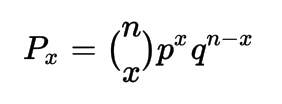PROBABILITY DISTRIBUTION
A probability distribution describes how the probabilities are spread out over different possible outcomes in a set of events. It can be discrete or continuous, depending on whether the variable it describes is discrete (like the number of heads in a series of coin flips) or continuous (like the height of people in a population).
There are two main types of probability distributions:
There are two main types of probability distributions:
- Discrete Probability Distribution:
- This type of distribution is associated with discrete random variables, which have specific, separate values. Examples include the probability distribution of the outcomes of rolling a six-sided die or flipping a coin.
- Probability Mass Function (PMF): For a discrete distribution, the probability mass function gives the probability of each possible outcome.
- Example: Consider the probability distribution for the sum of two six-sided dice rolls:
- Continuous Probability Distribution:
- Continuous distributions are associated with continuous random variables, where the variable can take any value within a range. Examples include the distribution of heights or weights in a population.
- Probability Density Function (PDF): For continuous distributions, the probability density function gives the likelihood of a random variable falling within a particular range.
- Example: The normal distribution (bell curve) is a continuous probability distribution with a probability density function.
Probability distributions must satisfy certain properties. For discrete distributions, the sum of the probabilities must equal 1. For continuous distributions, the area under the probability density function over the entire range must equal 1.
The specific probability distribution used often depends on the nature of the data and the underlying process being modeled.
Common distributions include the uniform distribution, binomial distribution, Poisson distribution, exponential distribution, and normal distribution.
Understanding probability distributions is fundamental in statistics and probability theory, as they provide a way to describe and analyze random phenomena and make predictions about future events.